Introduction
The purpose of the thesis is to provide a description of the “n-body problem”, both gravitational and electrostatic , and also, to provide a description of the solving methods available.
The thesis analyzes various versions of the Tree Code algrithm, by Appel, Jernigan and Porter and Barnes and Hut.Furthermore complexity analysis and error analysis are provided, as well as an examination and description of the data structures the algorithms use.The algorithms are compared on the basis of space simulation, hierarchical structure and algorithmic optimazation capabilities.
Algorithmic analysis and complexity analysis of the initial FMM method, and the Barnes-Hut method with matrices, as well as FMM with Rotation Matrices, as well as looking in to versions of FMM that try to optimize various aspects of the initial algorithm.
A number of short setup scripts are provided,as an example, so that with the minimum changes to the codes available by the various algorithm designers, the codes' performance can be assessed.Finally measurements and solution errors for a number of FMM solver programs are provided.
Comparison of Codes and Algorithms
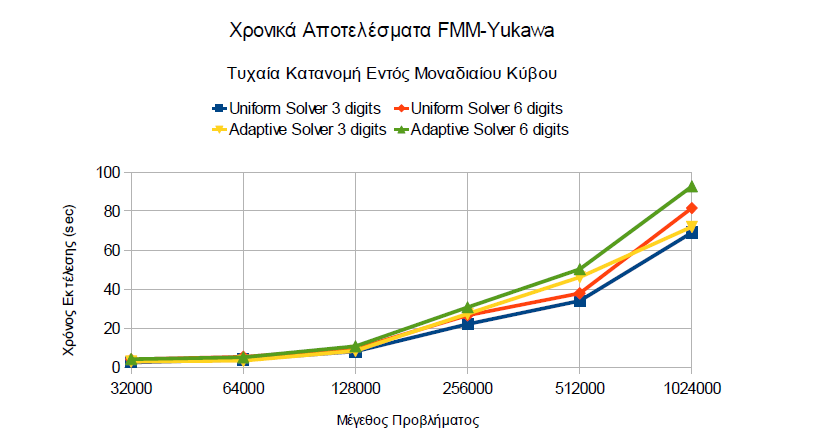
* FMM Yukawa Adaptive and Uniform Solvers
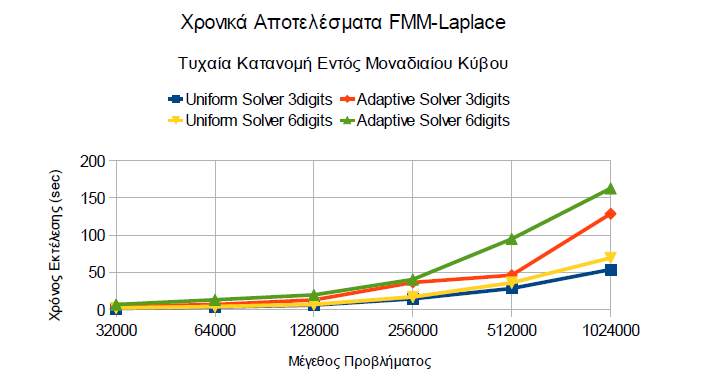
* FMM Laplace Adaptive,FMM Laplace Uniform, KIFMM3D and ExaFMM
* Splash_v2 FMM and Treecode (2d)
* Barnes-Hut Treecode
Results
FMM Yukawa Code
With build scripts, particle generators, and binary file loader functionality.